Dancefloor Equations: Fourier’s Mathematical Echo in Electronic Music
When you ask someone about their daily interactions with mathematics, many might mention everyday tasks like calculating grocery bills or managing monthly payments. However, stepping away from these basics for a moment, consider music—a medium most of us engage with daily. Yet, how often do we evaluate the mathematical intricacies behind our favourite tunes?
Exploring the relationship between mathematics and music, one might first think of the classical genre. It is filed with standing waves, harmonics, and even the mystical golden ratio—also known as the Fibonacci sequence—creating a complex mosaic of mathematical beauty. These elements, deeply rooted in nature and aesthetics, resonate through the majestic halls of classical compositions.
Fast forward to contemporary times, where genres have diversified, and electronic dance music (EDM) has surged in popularity. Today’s musical scene has shifted: it is less about waltzing to Chopin and more about moving to the rhythmic beats of techno, trap, ambient, and house. This new era of music introduces an unseen composer: Fourier analysis, orchestrating the beats that fuel today’s dance floors.

Image credit: Lucky170, CC BY-SA 4.0 DEED via Wikimedia Commons.

Image credit: Wellcome Collection, public domain via Wikimedia Commons.
Essence of Fourier Analysis
Fourier analysis is named after Jean-Baptiste Joseph Fourier, a notable French mathematician. The foundation for Fourier Analysis was laid by Euler, d’Alembert, and Bernoulli, who aimed to solve the differential equation of a vibrating string. This led to a significant debate about whether it is possible to represent an arbitrary function with a trigonometric series. Joseph Fourier, in 1807, made a landmark contribution by providing a solution to the one-dimensional heat equation using Fourier series, resolving the debate, and proving that this could indeed be done.
Fourier analysis is a mathematical method that breaks complicated functions into simpler ones with distinct frequencies.
There are two main parts: the Fourier series, which expand repeating functions into trigonometric functions, and the Fourier Transform, which does the same for non-repeating functions by transforming them from the time domain into the frequency domain. This displays different frequencies and how strong they are in the original function. A helpful analogy compares the Fourier Transform to determining the smoothie recipe; by deconstructing the smoothie, we can identify each ingredient and understand the composition more easily than if we tried to analyse the whole smoothie at once.
To grasp the application of Fourier transformation in music, it is essential to understand the nature of a sound wave. Imagine throwing a stone into the river, this creates ripples on the water’s surface. Similarly, sound produces disturbances in the air, akin to those ripples. These disturbances are caused by vibrating air particles that generate varying pressure points. Just as a thrown stone leads to a wave with peaks and troughs on water, particle vibrations in the air create waves that propagate forward. These waves, caused by the movement of air particles in the wave’s direction, enable us to perceive sound.
The image on the right visually represents a sound wave: (A) shows the air when it is still (i.e. no sound); (B) shows the pattern of a sound wave travelling through the air; and (C) representation of the wave across, amplitude (A) [maximum displacement] and wavelength (λ).
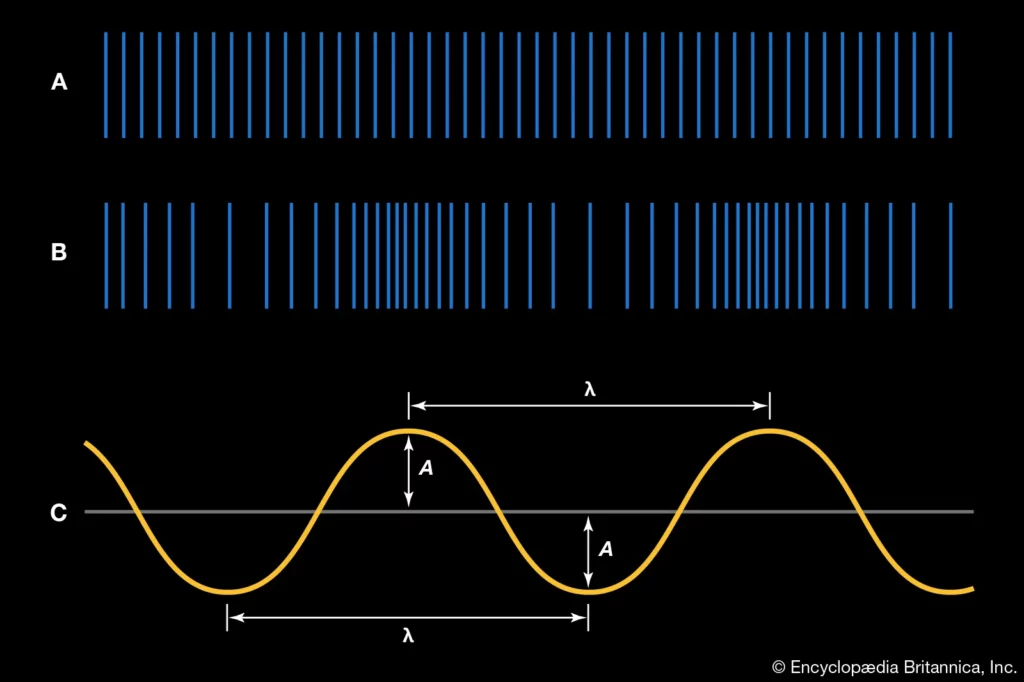
Image credit: fair dealing via Encyclopaedia Britannica.
The visualisation of Fourier Transformation applied to a sound wave demonstrates how Fourier Analysis is not merely a mathematical abstraction but a crucial instrument in the realm of music production. For music producers, it allows to dissect of complex sounds into their composing frequencies, much like cutting a multi-coloured tapestry to observe each thread. In EDM, this capability is critical for creating the genre’s signature sonic landscapes.
Fourier in Music Production and Song Identification
Techniques employed in EDM include Spectral Analysis, which uses Fourier analysis to translate a sound into a spectrum of frequencies, unveiling details imperceptible to the ear. This technique is embodied in spectrum analysers within Digital Audio Workstations (DAWs) – software used for recording, editing, and producing audio – providing a detailed graph of frequency over amplitude. This visual feedback assists producers in making informed decisions on equalisation, such as boosting or cutting specific frequencies to achieve clarity and balance in the mix. You might have even used this technique unknowingly. Ever searched for a song on Shazam?

Shazam identifies music using a digital fingerprinting process that relies on Fourier transformation. When a user records a song snippet, Shazam uses the Discrete Fourier Transform (DFT) to analyse the audio spectrum and identify distinct frequencies and timings, which constitute the song’s unique fingerprint. By comparing this fingerprint to a vast database of known songs, Shazam can identify the track despite the complexity of the audio or background noise. This Fourier-based method is fundamental to Shazam’s ability to detect and match a song’s identity efficiently.
Sound Design & Synthesis
If you have never tried to create sound samples or Disk Jockey (DJ) before, now is your chance, just click here and synthesise your own sounds via Wolfram Alpha.
Although it is by no means a tool designed to create a banger, it allows you to understand the fundamentals of sound creation, using techniques similar to those employed by music producers.
This application is based on the Fourier principle that any sound can be reconstructed by combining simple, rhythmic waves. By manipulating these waveforms with various parameters, a producer can craft a rich array of sounds, from natural instrument imitations to otherworldly electronic timbres.
Fourier’s Legacy
Mathematics and music share a profound and often underappreciated connection. From the ordered elegance of classical compositions to the pulsating heart of electronic dance music, mathematical principles serve as the backbone to the music we cherish. Fourier analysis stands out as a bridge between these two contrasting worlds. It enables us to deconstruct and reconstruct sound waves, offering music producers and listeners alike a deeper understanding and appreciation of the music that forms the soundtrack to our lives.
The legacy of mathematicians like Fourier is thus immortalized not just in equations and textbooks, but in every beat that moves us and every melody that resonates within us. As we go about our daily lives, often oblivious to the mathematics orchestrating our world, let us take a moment to listen closely—not just to the music itself, but to the maths that makes it possible. Whether through an app like Shazam or the synthesis of new sounds for a ground-breaking Television (TV) series, Fourier analysis continues to harmonise the notes of mathematics and music, inviting us all to explore the rhythms and patterns that control the art that moves us.
Author
Veronika Volodko

