Alice and Algebra
Lewis Carroll, (Charles Dodgson) Mathematician
Although known now as the writer of nonsense poems and children’s books, Lewis Carroll, the pen name of Charles Lutwidge Dodgson, was a mathematician. Born on 11 July, 1832 in Daresbury, England, Carroll lectured mathematics at Oxford. It was also at Oxford where he met an assortment of “child friends” or children whom he would babysit. One of these children was Alice Liddell, one of the daughters of Henry George Liddell, the dean of Christ Church. Many think that Alice’s Adventures in Wonderland is a direct copy of the story Carroll told Liddell on a sunny boat ride. This is not the case. The published version is full of hidden maths.
Image credit: Julie Hatfield, CC BY-SA 4.0
Image credit: Lewis Carroll, Public domain, via Wikimedia Commons
Image credit: Lewis Carroll, Public domain, via Wikimedia Commons
Logic and Maths in Alice
Carroll was a mathematical conservative. In the late 19th century, algebra was changing from pure numbers to symbols—symbolic algebra, if you will—and proofs were getting more colloquial. Most of the mathematics in Alice’s Adventures in Wonderland is a critique of the maths of the period! Let’s see some examples:
“Standard” Multiplication
Alice, seven years old, knows her times tables. But how is it that her times tables are so wrong? 4 times 5 isn’t 12, and 4 times 6 is definitely not 13.
But lo and behold, this is true! It works because of different bases. (You can learn more about different bases here!) This is when the concept of 4 times 5 might usually base 18 is 12, and 4 times 6 is 13 if the base is 21. Just for good measure, the formula for Alice’s puzzling multiplication is 4𝑛 in base 3+3𝑛, so 4 times 7 will be 14 in base 24. Poor Alice won’t ever get to twenty like this.
Image credit: Julie Hatfield, CC BY-SA 4.0
Caterpillars and Geometry
Today, the idea that algebra isn’t just about real numbers (1,2,3…) isn’t novel, but in the Victorian Era, this was a new development. Melanie Bayley wrote in The New Scientist that she believes the Caterpillar scene is actually about symbolic algebra—that is using algebra as a language, rather than just solving equations. (You can read more on symbolic algebra here!) Here’s why:
Image credit: Julie Hatfield, CC BY-SA 4.0
The first British treatise by Augustus De Morgan on symbolic algebra was translated from Arabic (the same language that the word “hookah” comes from) as “restoration and reduction” (from “al jebr e al mokabala”). That describes the chapter pretty well!
The Caterpillar tells Alice to “keep her temper.” He says being so many different sizes isn’t very hard. Alice doesn’t agree—and how would keeping calm help her right now anyways?
Intellectuals in Dodgson’s day would have seen the word “temper” differently. Rather, it means “a middle state between extremes.” So he’s actually telling her to keep proportional, or similar. In Euclidean Geometry, if the Caterpillar keeps his proportions, he’s still a Caterpillar, since magnitudes don’t matter, only ratios. (A big square is still a square, but a square with 2 longer sides and 2 shorter sides… that’s a rectangle!) However, when Alice goes out of proportion, we don’t know what she is! She meets a pigeon who asks if she is a “serpent” and she doesn’t know if that’s true! She could be. After all, snakes and little girls both eat eggs; one is just long. And Alice is long now too! But in symbolic algebra, can we say Alice is still a little girl?
Babies are Pigs and Cats Grin
Alice meets a baby in the house of the Duchess and the Cook with the Pepper. Or is it a pig? Pigs and babies are the same here in Wonderland, because they share the same “projected properties.” This has been read as a critique of the Principal of Continuity. Essentially, as long as the shape retains some of its basic properties, it can bend and shift into another shape. So, a circle is the same as an ellipse or a parabola, or the Cheshire cat’s weird, shifting grin. Since they retain the same principals, they are the same. A baby and a pig have the same number of limbs and holes and make similar noises, so they are the same.
But this is absurd! Dodgson cries from the background, because babies and pigs and the ever-present smile are not the same at all. But they are in topology!
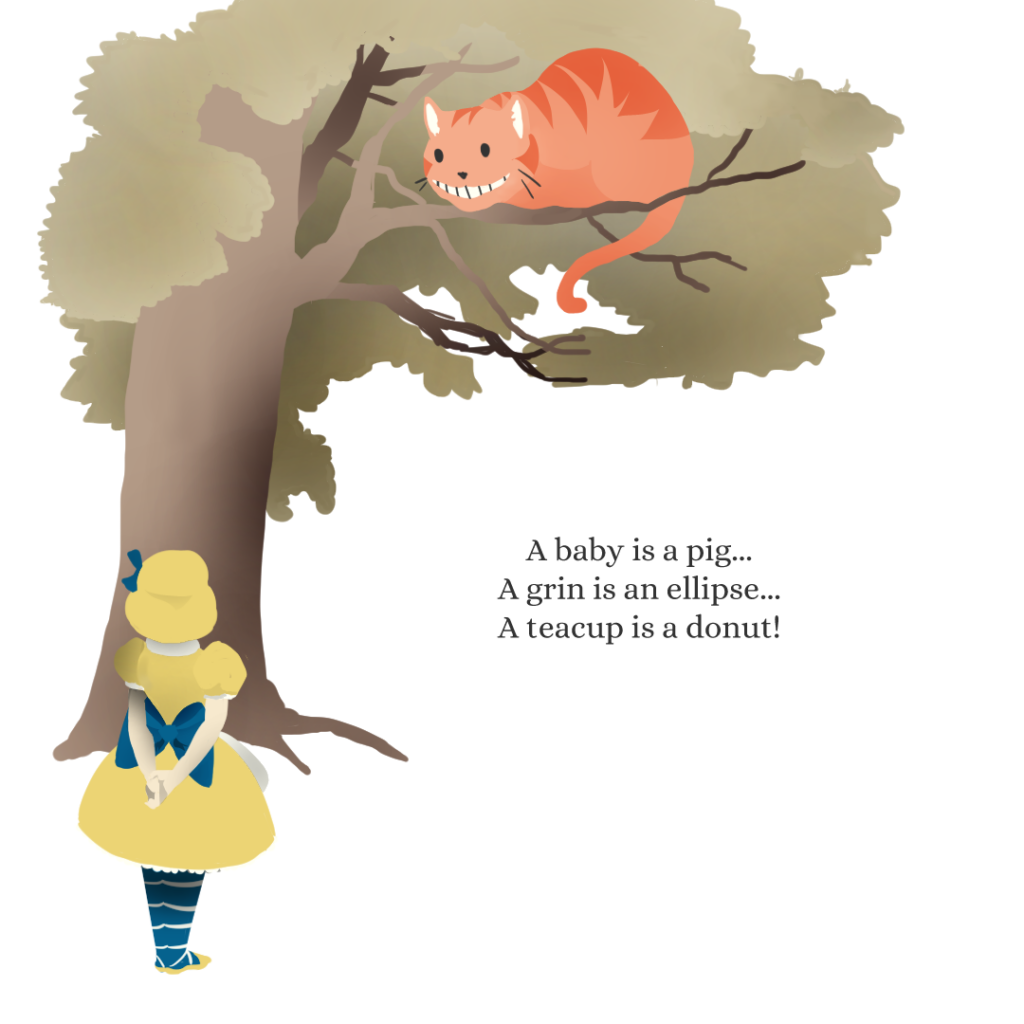
Image credit: Julie Hatfield, CC BY-SA 4.0
Image credit: Lucas Vieira, Public domain, via Wikimedia Commons
Image credit: Julie Hatfield, CC BY-SA 4.0
Mad t-Party
Finally, everyone’s favourite scene: the Mad Tea party. The Mad Tea party is a reference to the Quaternions! Quaternions are a type of algebra which describe rotations in a 3D space. (You can read more about quaternions here!) In 1843, when mathematician William Rowan Hamilton introduced Quaternions, they were being hailed by Victorians as changing abstract algebra forever. Hamilton began with only three terms, one for each dimension, and later added a fourth, which he called “Time.” Without time, the proposed Quaternions rotated on into infinity.
Early in the scene, the Hatter mentions that they’re missing a guest: Time! Without Time, they spend the rest of the day rotating around and around, until the Hatter and the Hare try to squeeze the Dormouse into the teapot. If they can get rid of another dimension maybe they would stop rotating. They wouldn’t be Quaternions anymore, at least.
Alice can’t stop the rotation, even when she joins the party. She’s not time and doesn’t have these special properties. See, Alice is commutative: she is the same forwards and backwards. The other three, however, are not! Their statements only work one way. She doesn’t fit into the group, and cannot replace the last, “noncommutative” element. Thus, despite her best attempts, she is unhelpful.
Lessons with the Turtle
Finally, there’s the lessons of the Mock Turtle. The Mock Turtle says that there are four new branches of arithmetic: ambition, distraction, uglification and derision. How mean! He talks of his lessons. Every day they lessen. Day one is ten hours, day two is nine, all the way to day eleven, which is a holiday.
“And how did you manage on the twelfth?” Alice asks. The Gryphon, also there, doesn’t want to talk about this. Negative numbers are hard to manage, after all. What happens for negative one hours? Do we gain it back?
If you want some more Lewis Caroll maths, how about you try some of his mathematical puzzles? Try them at here!
Author
Julie Hatfield
