Aryabhatiya of Aryabhata

Image credit: public domain via Wikimedia Commons.
Aryabhatiya: Maths in poetry
Aryabhatiya is a Sanskrit poem composed of 118 concise verses. Each verse states a mathematical or astronomical fact or algorithm, however, due to its succinct nature no proofs are shown. Additionally, puns are used to aid memorisation. That is the consequence of the privileged position of orality in Sanskrit literature. This tradition originated from Vedas, the oldest sacred text we know in India. It was believed that only a living teacher can teach the correct pronunciation of the sounds and explain hidden meanings, in a way the “dead and entombed manuscript” cannot do. Even treatises on secular and technical subjects were ideally considered as knowledge to be learned by heart, not merely kept in a book for reference.
Question about oral tradition
Dr. Anuj Misra gives another view, why should mathematicians in India abandon their tradition? We must realize that the statement “It is vital to have clear, unambiguous statement and fully explained proof.” is true only for mathematicians in the modern world and ancient Greece, historical actors in other parts of the world had different opinions. The Sanskrit tradition does not regard mathematical knowledge as providing a unique standard of epistemic certainty, it has been suggested that the corresponding role of “paradigmatic science” in Indian thought was filled instead by grammar. Therefore, ideas about reasoning and reality in Sanskrit philosophy and logic are explicitly linked to the understanding of linguistic statements. What philosophers need to probe is their grammatical interpretation rather than their analogies with mathematical entities. So, to sum up, Indian mathematician felt no discomfort with their tradition; they didn’t have reason to change it at that moment.
Aryabhata’s achievement
“Aryabhata is the master who, after reaching the furthest shores and plumbing the inmost depths of the sea of ultimate knowledge of mathematics, kinematics and spherics, handed over the three sciences to the learned world.” — Bhaskara I
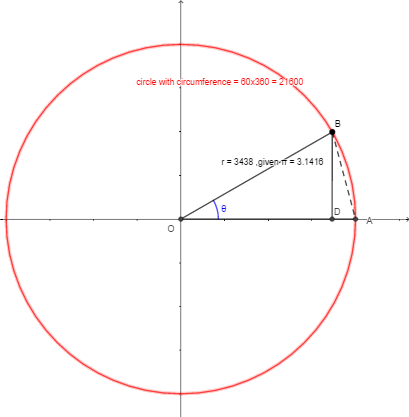
Image credit: Ammi Tian, public domain.
Aryabhata was very intelligent, his contributions include:
1. Invention of a place value system which is the base of Hindu-Arabic numeral system we use now.
2. Invention of an algorithm for solving first-order Diophantine equations.
3. Development of trigonometry, the name of ‘sin’ is in fact the wrong translation of the term ardha-jya, created by Aryabhata. And he gave out the first table of sines (though the Greek mathematician Hipparchus and his successor created tables of chord before him), which was widely used by Arabic and Persian mathematicians even 500 years later.
4. Approximation of π, accurate to three decimal places, and probably the first time in the world that it was spotted π is not rational. He specifically states that the value is approximated, but we could not learn more as the relevant statement is too short.
5. Developed a heliocentric model. While the Greeks believed the sun rises because of its revolution around earth (read more about this in the Ptolemy’s Geocentric Model article), Aryabhata correctly stated that is due to the rotation of earth, and earth also revolves around the sun. What makes it even greater is that, as far as we know, he was the first one to state the orbits of planets are elliptical, that is 1000 years before Kepler.
Even the wise are not free from error
However, Aryabhata made several mistakes in his book: the definition of a square, calculation of the volume of a pyramid and sphere.
The definition of a square in his book is stated as:

Image credit: public domain.
“2.3.ab. A square is an equi-quadrilateral, and the area/result is the product of two identicals.”
Here ‘equi-quadrilateral’ means 4 sides are equal, but this definition also includes rhombuses, whose area is not the product of identical sides. His successor Bhaskara I, also a later commentator on the Aryabhatiya, fixed it by adding equal diagonal to definition.
The mistake in volume calculation was due to Aryabhata simply using the hypothesis: the solid equilateral is seen as deriving geometrically from the area by the same process that derives a surface from two lines. In other words, he just applied the experience of planar figures to a higher dimension.
He recorded that the volume of a sphere generated by a circle is , where ‘A’ is the area of that circle, but the true formula is
And for the volume of a pyramid (i.e., tetrahedron, Aryabhata named it as ‘twelve edged’), he thought the volume should be , ‘A’ being the area of the base triangle, ‘h’ the length of height that perpendicular to base and cross the summit point. While the true formula is
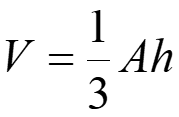
We can see that the cubic relation is correct in those two formulas, but the constant coefficient is wrong. That means they can be easily fixed with enough data support. Unfortunately, ancient India lacked the ability to measure volumes of non-cubic solids, while the Greeks could use Archimedes‘ principle (any body completely or partially submerged in a fluid is acted upon by an upward force which is equal to the weight of the fluid displaced by the body).
Acknowledgement
I would like to express my sincere gratitude to my supervisor, Dr. Isobel Falconer, for her guidance.
I am also very grateful to Dr. Anuj Misra, for his constructive comments and suggestions that helped me improve the quality of my work.
Katz, Victor J., ‘The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook’, (Princeton, 2007).
Keller, Agathe, ‘Expounding the Mathematical Seed. Vol. 1: The Translation: A Translation of Bhāskara I on the Mathematical Chapter of the Āryabhatīya’, (Basel, 2006).
Misra, Anuj, ‘Sanskrit Mathematics in the Language of Poetry’, The Annual BSHM Gresham College Lectures, Gresham College, 20 Oct 2021, <https://www.gresham.ac.uk/watch-now/sanskrit-mathematics> [accessed 20 March 2023].
O’Connor, John J.; Robertson, Edmund F., “Aryabhata”, MacTutor History of Mathematics archive, University of St Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Aryabhata_I/# , accessed 11/03/2023.
Plofker, Kim, ‘Mathematics in India’, (Princeton, 2009).
Author
Ammi Tian

