Hippasus and Irrational Numbers
Greek mathematician Hippasus is believed to have died because of the discovery of irrational numbers, those numbers could not be expressed as the ratio of 2 integers, for example, √2 , while in China, such numbers are called “面”, which can be translated to “noodle”. However, there are still lots of mysteries in this story.
Who is this mathematician?
Hippasus of Metapontum, a Greek mathematician and philosopher, who probably lived in the late 5th century BC, is widely believed to have been the first to discover irrational numbers, and to have died for achievement, either as divine retribution by the Gods, or put to death by his fellow Pythagoreans.
As a Pythagorean philosopher, he was cited by Aristotle in <Metaphysics>, and Diogenes Laertius <in Lives of Eminent Philosophers>, so his brilliance is certain.
Unfortunately, as a mathematician, there are only a few contradictory and ambiguous legends about him. The first question is about his birth. Iamblichus (a philosopher in about 3rd century AD) wrote in <On the Pythagorean way of life>: “Some say Hippasus was a Crotoniate, others that he was a Metapontine.”

What has he done as mathematician?
The discovery of irrational numbers is attributed to Hippasus by many modern authors, including Morris Kline and Kurt Von Fritz; however, there isn’t any known direct evidence that is strong enough to support that proposition.
Iamblichus also said “the one who broke the news about the irrational and incommensurability [could be considered as another name of irrational] suffered this fate [perished in sea]” precisely what happened to Hippasus. Pappus, a mathematician during the same period, echoed this statement in his <Commentary on Book X of Euclid’s Elements>. There are still two problems with the statement that he discovered irrational numbers:
- What happened on Hippasus was 700 years earlier than the legends told by Pappus and Iamblichus, so their accuracy is debatable.
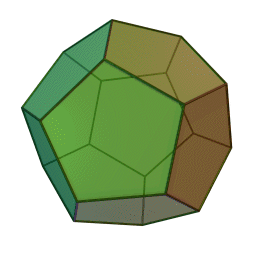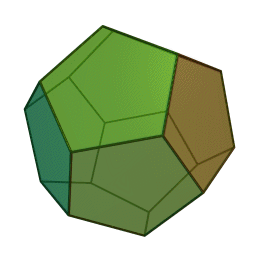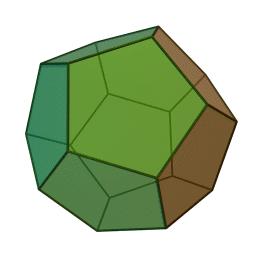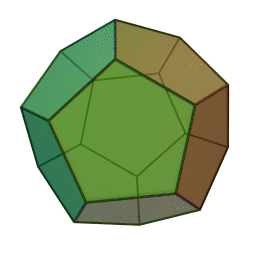
- Even if we believe their legends are based in fact, neither writer related Hippasus to be the one that discovered irrational numbers – the only clearly stated mathematical achievement of Hippasus was his diagram of a dodecahedron inside a sphere, the first of its kind, and he perished in the sea for different reasons. Iamblichus said in his book:
“On the matter of Hippasus in particular: he was a Pythagorean, but because of having disclosed and given a diagram for the first time of the sphere from the twelve pentagons, he perished in the sea since he committed impiety. He acquired fame as having made the discovery, but all the discoveries were of that man, for so they refer to Pythagoras, and do not call him by his name.”
Perhaps there is a way to resolve these differences: Hippasus did indeed discover irrational numbers when constructing a dodecahedron. However, the most precise way to deal with this problem is to abandon statements that lack evidence.
Why did he die?
Despite the disagreement over irrational or dodecahedron, his death is certainly a consequence of impiety in all versions of the legend. In some versions it is the Gods themselves who ensure that he drowns (for example by creating a storm), whereas in others it is Pythagoras’ followers. So, one certain thing is he was hated by Pythagoras’ followers, a characteristic of the Pythagorean school is mixing mysticism with mathematics, there are lots of examples where zealous followers persecute innocent people just because of religious taboos.
The reason why Pythagorean theory forbade irrational numbers can be found in Aristotle’s <Metaphysics>: “they assumed the elements of numbers to be the elements of everything, and the whole universe to be a proportion or number”
While the “number” here only includes rational numbers, whcih could be expessed as the form p/q, p and q are natural numbers, dating to Hippasus’ time, the most serious problem of irrational numbers is that they are inexpressible. Greek numerals are not independent symbols as in other civilizations; they just put a bar on the letters to represent positive integers, add another mark on integers to represent unit fractions, and use the sum of unit fractions to represent other rational values. This type of expression limits the acceptance of irrationals. The existence of irrational number contradicts some propositions of Pythagorean schools (we couldn’t know if these propositions belong to Pythagoras himself, but it is reasonable to assume so because adherents are often sensitive about that).
“Noodle”?
In a famous Chinese mathematical treatise <The Nine Chapters on the Mathematical Art> (九章筭术), which originated before 212 BCE according to Liu Hui’s commentary, the square root which are not integer, including √2, is called “面” : 若开之不尽者为不可开,当以面命之.
This sentence is translated as “If there is a remainder, [the number] is called unextractable” by John N. Crossley and Anthony W.-C. Lun. Here the “unextractable” correspond to “面”; however, it is not totally accurate, since “面” is a noun, while “unextractable” is an adjective. Its literal translation could vary in different situations: “noodle”, “face”, “surface”, “side”… The most suitable translation here should be “side”, suggested by Joseph W. Dauben, because the geometry behind extracting square roots is finding the side of a square. In contrast to the Pythagorean school, ancient Chinese mathematicians simply accepted the fact that irrational numbers exist, though it is debatable whether they realized the properties of irrationals.

Irrationals after Hippasus
As V said in the film <V for Vendetta>: “ideas are bulletproof!”, murder couldn’t stop the truth. We know from Plato’s work <Theaetetus> that there still were mathematicians that dared to study irrationals: Theodorus and Theaetetus, who were associates of Plato’s, proved the irrationality of the square roots of some numbers from 3 up to 17. Additionally, Pappus recorded that Eudoxus ended the conflict of irrationals by developing a theory of proportion though a definition that allowed irrational lengths to be compared in a similar way to the method of cross multiplying used today. Fortunately, no one would die due to “noodle” anymore.
Author
Ammi Tian

