Kenneth Arrow’s Impossibility Theorem in Social Choice Theory
Kenneth Arrow’s Impossibility Theorem is an important work in the field of Social Choice Theory. Are his insights into the fairness of various systems of voting valuable in the real world? If not, how can we apply alternate insights from Social Choice theory to determine a mathematically proven system of voting?
Situating Arrow within the discipline of Social Choice
What makes a vote ‘fair’? Are some voting methods preferable to others? Is it possible for a vote to yield a truly democratic result?
These are questions which Nobel Prize winning economist Kenneth Arrow grapples with in his famous publication ‘Social Choice and Individual Values’ (1st ed. 1951; 2nd ed. 1963). Arrow’s work is based within the discipline of Social Choice Theory: the study of how a collective (an electorate, legislature, or jury, for example) can arrive at a decision which best reflects the preferences of its individual members.
Social Choice is not a single theory, but rather a group of models and results, containing insights from both natural and social sciences. The discipline has certainly expanded over time to draw knowledge from an ever-broader range of subject areas. Mathematics has remained integral to Social Choice Theory for all its existence, providing the essential tools for judging the effectiveness of different methods of grouping together individuals’ preferences.
The importance of mathematical methods to Social Choice Theory is easy to see in Arrow’s work. The logic of his argument in ‘Social Choice and Individual Values’ heavily relies on set notation and mathematical proofs for clarity of expression.

Image credit: Stanford News Service, CC BY 3.0 DEED via Wikimedia Commons.
Insights from the past
At the core of ‘Social Choice and Individual Values’ is what Arrow refers to as the ‘General Possibility Theorem, more widely known as Arrow’s Impossibility Theorem.
The theorem establishes, to paraphrase, that no voting system which requires voters to rank three or more alternatives according to their preferences, can satisfy all the criteria for fairness laid out by Arrow.
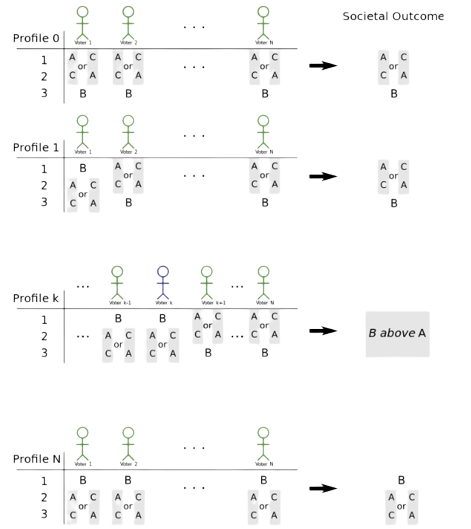
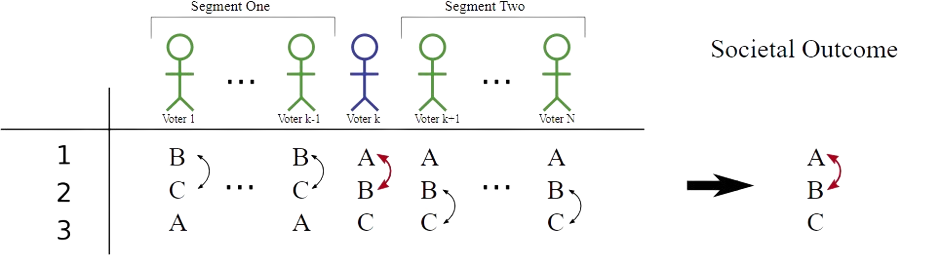
Image credit: Niles Johnson, CC BY 3.0 DEED via Wikimedia Commons.
Arrow’s focus here is on ordinal voting systems, in which individuals vote by ranking alternatives according to their preferences. Arrow uses the term ‘alternatives’ to denote the different viable options from which a society must choose (individual candidates, political parties etc.), ‘society’ for the collective name for a group of individuals. Different methods of gathering and organizing individuals’ ranked preferences are referred to by Arrow as ‘Social Welfare Functions’ (SWFs).
There are five conditions which Arrow uses to judge the ‘fairness’ of ‘Social Welfare Functions:
- Unrestricted Domain (U): the SWF must be able to account for any order in which individuals might rank their preferences.
- Pareto Property (P), taken from the work of economist Vilfredo Pareto: if all individuals unanimously prefer one alternative (A) to another (B), then that one alternative (A) will be socially preferred to the other (B).
- Independence of Irrelevant Alternatives (IIA): if all individuals in a society rank one alternative (A) above another (B), then the ranked societal preference will also rank that one alternative (A) above the other (B), irrespective of any differences in individuals’ ranking of other alternatives (C, D, E, …).
- Non-dictatorship (ND): There is no single member of society, for whom the aggregated societal ranking of alternatives is identical to their own individual ranking.
- Transitivity (T): for any profile, if one alternative (A) is socially preferred to another (B) and this second alternative (B) is socially preferred to a third (C), then A must be socially preferred to C.
By modelling different combinations of these conditions, Arrow concludes that there is no Social Welfare Function which can satisfy all of U, P, IIA, ND and T. From this, Arrow’s Impossibility Theorem is often described as a mathematical proof of the impossibility of populist democracy, meaning a system in which the will of the electorate is faithfully transferred to public policy. A less sweeping conclusion to be drawn from Arrow’s theorem would be that it proves, not against the possibility of democracy, but against the existence of a perfect voting method.
Criticisms of the Impossibility Theorem
The impact of Arrow’s Impossibility Theorem on Social Choice Theory has been broad and long-lasting. This is shown through works that cite Arrow and, more significantly, the number of proofs and theories produced in direct response to the Impossibility Theorem. The volume of discourse which Arrow’s work has generated also points to some serious flaws in his theorem.
Criticisms of the Impossibility Theorem are centred around the five conditions for fairness that Arrow establishes. The non-dictatorship (ND) condition has been particularly heavily criticised, many arguing that all preference aggregation methods can be classified as dictatorial based on the definition which Arrow provides. Criticisms of the IIA condition are based around its pairwise conceptualisation of alternatives- only ever comparing them in sets of two- which makes this condition relatively incompatible with Arrow’s transitivity (T) condition, transitivity requiring the consideration of a complete set of alternatives.
Insights from the past
It is also possible to build upon Arrow’s findings by considering historic examples of Social Choice Theory. The ‘relative majority rule,’ proposed by 18th Century French philosopher and mathematician Condorcet, addresses ordinal voting systems and states that one alternative (A) will rank above another (B) in the ordering of societal preferences, where the number of ballots ranking A above B is greater than the number of ballots ranking above B (n(AB)>n(BA)). This rule has the potential to create a ‘paradox of voting,’ because is possible for an electorate to rank alternative A over B, alternative B over C, and alternative C over A, all in one ballot. The so-called ‘cyclical majority’ this creates violates Arrow’s transitivity condition.
While Condorcet’s rule is in no way perfect in comparison to Arrow’s Impossibility Theorem, it does satisfy the other conditions of Arrow’s ‘Impossibility Theorem’ over a more extensive domain of profiles than any other aggregation rule. Furthermore, empirical research into the results of ordinal votes on various scales has shown in practise that cyclical majorities are not particularly common. This is especially the case where a large set of individuals chooses from a small set of alternatives as in presidential or parliamentary elections, with such cases often being the main point of reference for Social Choice Theory. Condorcet’s majority rule therefore does not always prove intransitive, pointing towards it being an optimal method of preference aggregation under Arrow’s conditions for fairness.
Kenneth Arrow’s ‘Social Choice and Individual Values’ can be seen as both a seminal work in the discipline of Social Choice Theory and a triumph of mathematical methods, with Arrow’s attempt to model the ranking and aggregation of individuals’ voting preferences. The ‘Impossibility Theorem’ however, fails to provide a definitive answer as to which voting methods are preferable to others, with further issues arising from the conditions which Arrow uses to define a voting system as fair. Only through application of historical examples of Social Choice Theory, has Arrow’s theorem provided relevant insights into real-life voting situations.

Image credit: Wellcome Collection, CC BY 4.0 DEED via Wikimedia Commons.
Author
Lucy Wilson

