Liu Hui vs Archimedes: 𝜋 algorithm
Liu Hui’s 𝜋 algorithm essentially uses the area of a polygon inscribed in a circle to approximate the area of the circle. The more sides are added to the polygon, the more accurate the approximation evolves. It is remarkable that, although Liu Hui should have developed his algorithm entirely independently from the western world, it shares a great similarity to Archimedes’ approach, which is the first algorithm ever created to calculate 𝜋 and uses the perimeter of the inscribed polygon to approximate the circumference of the circle. Both algorithms share a vision in using the concept of limit and infinity. Great minds think alike!
In more detail, both algorithms use a lower limit and an upper limit to narrow down the value of 𝜋. In both cases, the lower limit is represented by the inscribed polygon. However, when it comes to the upper limit, there is a difference that gives Liu Hui’s method an advantage in accuracy: instead of using a circumscribed polygon like Archimedes did, Liu Hui used rectangles extended at each side of the inscribed polygon, with width equal to the length of the side and height equal to the ‘excess radius’ made by the polygon (the height of green triangles in the graph). While in 250 BC Archimedes used his approach and a 96-sided polygon to prove that 223/71 < 𝜋 < 22/7 (i.e., 3.1408 < 𝜋 < 3.1429), in 265 AD Yang Hui used his method with a 3072-sided polygon to obtain that 𝜋 ≈ 3.1416. Both results were a world record during their respective times!
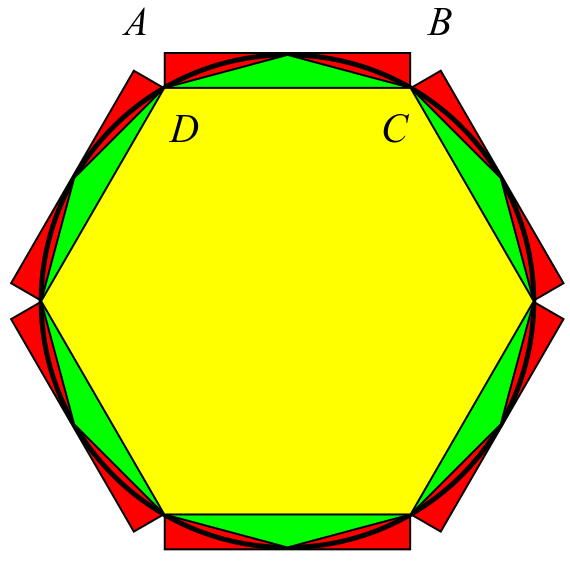
Image credit: derivative work: Pbroks13 (talk) Liuhui_Pi_Inequality.jpg: Gisling, CC BY-SA 3.0, via Wikimedia Commons
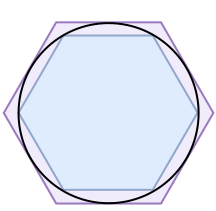
Image credit: derivative work: Yansong Li, Original: Fredrik, Vector: Leszek Krupinski, Public domain, via Wikimedia Commons
Zu was very familiar with Liu Hui’s algorithm, and it is speculated that Zu came up with an effective method to simplify square root computation in his calculations, because otherwise these calculations would have taken an almost impossible amount of efforts to work out. However, his mathematical book Zhui Shu (缀术; Method of Interpolation), which recorded how he exactly calculated 𝜋, was lost in the early twelfth century, being too complicated and advanced for other people at the time.
Borwein, Jonathan Michael, The life of 𝜋: from Archimedes to ENIAC and beyond (Heidelberg, 2014).
Boyer, Carl Benjamin, A History of Mathematics (New York, 1991).
Mikami, Yoshio, The Development of Mathematics in China and Japan (Leipzig, 1913).
O’Connor, John Joseph and Robertson, Edmund Frederick, ‘Zu Chongzhi’, MacTutor History of Mathematics Archive, Website, <https: mathshistory.st-andrews.ac.uk/biographies/zu_chongzhi/> [accessed 19 February 2023].
