Maths Symbols
In the modern world, many of the commonly used mathematical symbols will be recognised and understood across most countries. However, this was not always the case. For much of history, most places had no symbols for many of the most common operations such as addition and subtraction. Instead, they relied on words. It was not until the 14th Century that the addition symbol we have today came into use, whilst many of the other everyday symbols seen today weren’t created until over 100 years after this.
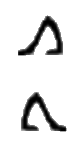
The Egyptian hieroglyphic symbols for add and subtract.
Image credit: public domain.
Addition and Subtraction
In Egyptian hieroglyphics, addition and subtraction were denoted by symbols that resembled a pair of legs walking either forward to represent addition and backward to represent subtraction. In the 15th Century, French mathematician Chuquet used “p” to denote plus and “m” to denote minus. Similar symbols, but with a straight line above the “p” and “m” were also used after being introduced by Italian mathematician Luca Pacioli in 1494.
The current symbol for addition, +, has its origins in the Latin “et”, meaning “and”. It is widely believed that Nicole Oresme, a 14th century French philosopher, may have been the first to use + in approximately 1360.
Whilst the origin of the subtraction symbol, -, is uncertain, there are a range of theories to suggest its emergence. Some say that the symbol is derived from an Egyptian hieratic sign, whereas others say was derived from an early way of using a bar to represent an M.
The first recorded use of the subtraction symbol in algebra can be found in a German manuscript from 1481. Whilst the symbol is the same that we use today, it was often found after the number rather than before. For example, -4 could be written as “4 das ist –“ (4 this is -), meaning to subtract 4.
It was in Johannes Widmann’s 1489 work Behende und hübsche Rechnung auff allen Kauffmanschafften (quick and neat calculation on all kinds of trade) that saw the first use of the addition and subtraction symbols in print. Here, he wrote “Was – ist das ist minus und das + das ist mehr” (that – refers to minus and + refers to more). However, these symbols likely had a slightly different meaning, being used to represent surplus and deficient regarding warehouse goods.

Image credit: Johannes Widmann, public domain via Wikimedia Commons.
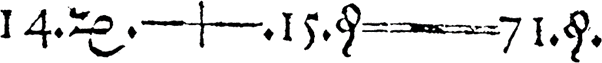
Image credit: Robert Recorde, public domain, via Wikimedia Commons.
Equals
Before the equals symbol we commonly use today was created, the world saw many different versions and notations meaning ‘equal to‘, including ‘pha‘, which was used by mathematicians from India in around 900 BC, and a blank space, used by the Italian mathematician Gerolamo Cardano in 1539.
The first recorded use of = was by Welsh mathematician Robert Recorde in his 1557 work The Whetstone of Witte, which was also the first in English to use the addition and subtraction symbols. Whilst the symbol Recorde used was much longer than the symbol used today, the basic concept is the same. To avoid the repetition of “is equal to”, he decided to use two parallel lines because, in his view, “no two things can be more equal”. However, despite its introduction, its use did not become commonly accepted until the 18th Century. Instead, symbols such as || and ∝, from the Latin ‘aequalis’, meaning equal, were used by many.
Multiplication
Like the other operations, many other symbols were used before the one we see today came into use. For example, the letter M has been used by many throughout history, including Michael Stifel, a German monk and mathematician, in his 1945 book Deutsche Arithmetica.
The symbol we commonly use today is often referred to as the St. Andrew’s cross. Whilst this cross has been used for a variety of operations since medieval times, such as for the addition and subtraction of fractions, it was William Oughtred who is commonly accepted as the first person to use it for multiplication in his 1631 work Clavis Mathematicæ. Furthermore, it is possible that Oughtred also used this symbol 13 years earlier in an anonymous 1618 appendix to John Napier’s work Mirifici Logarithmorum Canonis Descriptio (the Description of the Wonderful Canon of Logarithms).
However, not everyone agreed with the use of the cross for multiplication. For example, in 1698, German mathematician Gottfried Wilhelm Leibniz proposed the use of the dot,⋅ , for multiplication as the St. Andrew’s cross was too similar to the letter X. The dot symbol is still used in many countries across the world.

Image credit: John Napier, public domain, via Wikimedia Commons.
Division
Before the first use of the division symbol in use today,÷ , many different symbols were used. Michael Stifel used a closed bracket in his 1544 work Arithmetica integral, whereas Gottfried Wilhelm Leibniz used a colon to represent both fractions and division in the scientific journal Acta eruditorum, published in 1684.
The use of this symbol to denote division first appeared in the 1659 algebra book Teutsche Algebra by Johann Rahn. However, it is believed that it was the book’s editor John Pell who had been the one to introduce this symbol.
Despite its widespread use to mean division, the ÷ symbol has still recently been used to represent other operations. For example, Ernst Westerlund Selmer, a Norwegian professor, published work in 1921 containing “0,72 ÷ 0,65 = 0,07”, where the division symbol is used for subtraction, and the commas are used as decimal places, a practice which is still common today.
Atkinson, Leigh, ‘Robert Recorde and the Meaning of “Is”’, Math Horizons, 19: 1 (September 2011), pp. 20-22.
Cajori, Florian, A History of Mathematical Notations, (New York, 1993).
Cajori, Florian, William Oughtred, (Frankfurt, 2018).
Kreiling, Frederick C., ‘Leibniz’, Scientific American, 218:5 (May 1968), pp. 94-101.
Malcolm, Noel and Stedall, Jacqueline, ‘John Pell and His Correspondence with Sir Charles Cavendish’, The Mathematical Intelligencer, 19: 1 (December 2007), pp. 57-59.
Napier, John, Mirifici logarithmorum canonis descriptio, (1614).
Recorde, Robert, The Whetstone of Witte, (1557).
Stallings, Lynn, ‘A Brief History of Algebraic Notation’, School Science and Mathematics, 100: 5 (May 2000), pp. 225-269.
Widmann, Johannes, Behende und hupsche Rechnung auf allen kauffmanschafft, (1489).
Author
Andrew Maughan

