Ptolemy’s geocentric model
It is not rare that people make mistakes in maths; the frustration caused by those mistakes sometimes torments people a lot. Here is one fact that might relieve the frustration: even the smartest and best mathematicians make huge mistakes, and that does not damage their fame. In fact, Ptolemy, a Greek mathematician who lived in the 2nd century, is famous for his geocentric model which consists of tons of mistakes.
Praise across the world
You may wonder why these experts praise Ptolemy’s geocentric model which has long since been dumped into the trash bin of discarded theories? The answer is that Ptolemy’s Almagest, more than any other book, convinced people that the seemingly complex phenomena of the heavens could be represented by a simple underlying mathematical description. Although there are evidences showing that positions of celestial bodies and the times of celestial events could already be predicted by Babylonians and Chinese centuries before Ptolemy, he firstly use maths to give out a clear ontological reference, before him, maths is only limited to the calculation for the prediction of certain astronomical phenomena rather than models that correspond. Harnessing untamed nature into a mathematical theory is not a simple task, because observational data are not quite as tidy as the abstractions of pure points and lines, but Ptolemy eventually achieved that.
Models and Mistakes

Image credit: Theodor de Bry, public domain, via Wikimedia Commons.
In Book I of Almagest, Ptolemy introduced his model: “the heaven is spherical in shape, and moves as a sphere; the earth too is sensibly spherical in shape, when taken as a whole; in position it lies in the middle of the heavens very much like its centre; in size and distance it has the ratio of a point to the sphere of the fixed stars; and it has no motion from place to place.” Despite some inconsequential problem, such as the centre of universe, there are two important mistakes that he made. Firstly, the rotation and revolution of Earth are omitted (which is the reason for lots of other mistakes), secondly planets move elliptically around the sun, not circularly around the Earth.
Differing from the public’s stereotypical perception, those mistakes in his geocentric model are not the consequence of religious pressure. It is true that a Stoic philosopher is reported by Plutarch to have thought that the Greeks ought to indict a heliocentric scholar for impiety for putting the ‘hearth of the universe’ [the Earth] in motion. But there is no evidence to show that Ptolemy was influenced by Stoics or Christianity which was only legalized in the Roman empire about 15 decades later. Conversely, those mistakes are a consequence of logic: Ptolemy fully evaluates his assumptions with pros and cons before he made it the foundation of model.

Image credit: Bartolomeu Velho, public domain, via Wikimedia Commons.
Four centuries before Ptolemy, Aristotle had already recorded the existence of gravity in his On the Heavens: There is a unique movement of most matters, excluding air, clouds etc., toward the centre of our planet. So naturally, he stated:
“The place to which any fragment of earth moves must necessarily be the place to which the whole moves; and in the place to which a thing naturally moves, it [Earth] will naturally rest.”
Ptolemy agreed with Aristotle’s opinion, although he stated that the rotation of Earth could also explain all the movements in the heavens:
“…supposed the heavens to remain motionless, and the earth to revolve from west to east about the same axis [as the heavens], making approximately one revolution each day…”
But he quickly denied that in a long argument with several reasons, one of which I give below:
Ptolemy’s argument seems reasonable under the assumption that clouds are unaffected by gravity, which is the reason why clouds are floating in Aristotle’s explanation.
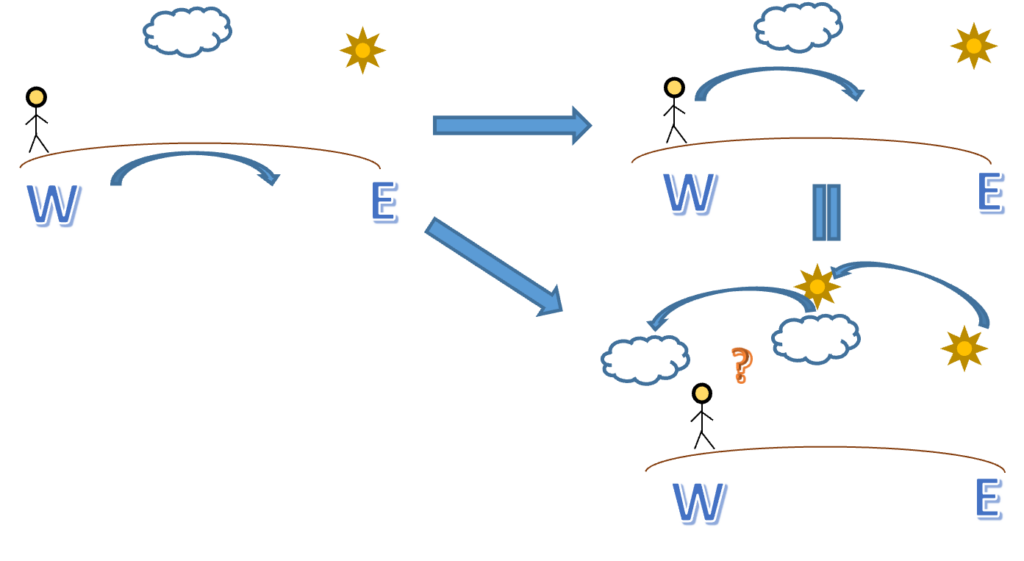
Image credit: Ammi Tian, CC BY-SA 4.0.
Under the condition that the Earth is not moving, most of the other mistakes come as a consequence. The daily appearance of celestial bodies is then regarded as the revolution around Earth. Ptolemy deduced the wrong conclusion using a wrong assumption:
End of geocentric model
Although Ptolemy‘s model has been discarded, his work can still inspire people: it is not shameful to make mistakes, just try your best and let the merits outweigh the flaws.
Gingerich, Owen, ‘Islamic Astronomy’, Scientific American, vol. 254, no. 4 (1986)
Heath, Thomas, A history of Greek mathematics (Oxford, 1921)
Netz, Reviel, A new history of Greek mathematics (Cambridge, 2022)
Ptolemy, Claudius, ‘Almagest’ (Alexandria), translated by G. J. Toomer (New Jersey, 1998)
Walbank, F. W., A. E. Astin, M. W. Frederiksen, and R. M. Ogilvie, eds. The Cambridge Ancient History Volume 7, Part 1: The Hellenistic World, 2nd edition (Cambridge, 1984)
Author
Ammi Tian

