Quaternions
What are the Quaternions?
The Quaternions are a number system invented (discovered?) by William Rowan Hamilton which represent the dynamics of 3D space. They are generally written in the form a + bi + cj + dk, and where a, b, c, and d are real numbers and i, j, and k are basis vectors (which means they’re somewhat akin to variables in the fact they can only be added between one another, where i can only be added to elements of i, j only to j, and so on.)
Thus (a + bi + cj + dk) + (e + fi + gj + hk) = (a + e) + (b + f)i + (c + g)j + (d + h)k.
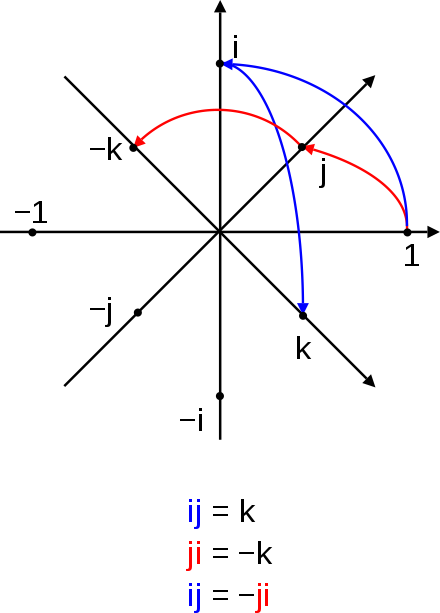
Image credit: Unknown, Public domain, via Wikimedia Commons
What makes quaternions different from other vectors with 3 dimensions is their interesting non-commutative (doesn’t give the same result forwards and backwards) multiplication. It can be summed up through this chart here:
| × | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
Hence, 2j × 3k = 6i but 3k × 2j = -6i. Additionally, multiples like, j × j = -1.
This can be represented visually by images such as:
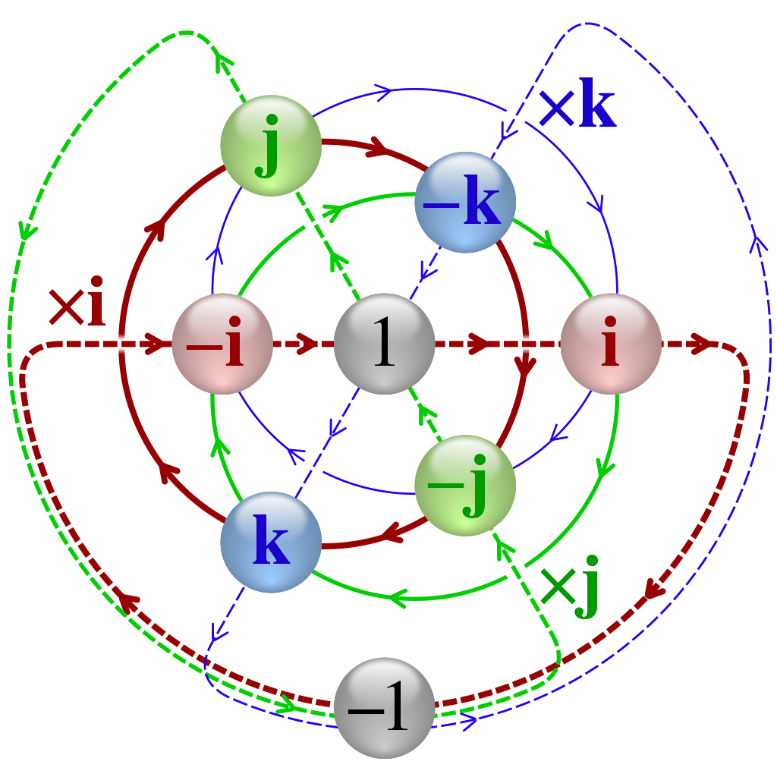
Image credit: Cmglee, CC BY-SA 4.0, via Wikimedia Commons
What’s the point?
Quaternions are especially useful for describing a 3-dimensional space. (You can roughly think of each of the basis vectors as a special version of x,y,z and the 1 as time, as Hamilton theorised.) Anything that can be rotated, stretched or pulled is theoretically described by the quaternions! Although usurped by simpler vector analysis in the later 19th century, quaternions have had a renaissance since the late 20th century due to computing.
Quaternions are especially useful for computer graphics: for example Nasa’s WorldWind, which creates graphics of geospatial data. Quaternions are also utilised in missile and aircraft targeting computer systems. Additionally, they’re found in electric toothbrushes!
If you want to play around with a graphical representation of the quaternions, you can try it out here!
O’Connor, J.J. and Robertson, E.F. (1998) William Rowan Hamilton – Biography, Maths History. Available at: https://mathshistory.st-andrews.ac.uk/Biographies/Hamilton/ (Accessed: March 29, 2023).
Author
Julie Hatfield
