Roman Numerals
The Roman empire was one of the most influential civilisations in world history, and one of its most enduring legacies is its numerals.
From the Super Bowl to monarchs, from years to chords, from your own name to the face of a clock, they are visible in every part of society as an aesthetic symbol of classiness. But how do they work? Where did they come from? And how were they used?
How do they Work?
The Roman number system assign symbols to the numbers 1, 5, 10, 50, 100, 500, 1000 as shown in the table below. For numbers larger than this, a horizontal line would be placed over the symbol to signify it should be multiplied by 1000. This allows us to express values up to 4,999,999. The largest value is written first, with smaller values following until the full number is written as the sum of the values. For example, the number 73 would be written as LXXIII, with the L representing 50, XX representing 20, and III representing 3. In a contemporary example, the Super Bowl is (normally) marketed using Roman numerals, with the most recent one being LVII. As the L represents 50, V represents 5, and II represents 2, this was the 57th such game. There are some exceptions to this. For example, instead of the numbers 4 and 9 being written as IIII and VIIII, they are written as IV and IX as they are one off the next symbols value. In general, no numeral should appear more than three times when writing any one number.

Image credit: Barry Mangham, CC BY-SA 3.0 DEED via Wikimedia Commons.
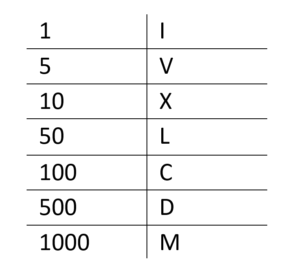
Image credit: public domain via Ben Tocher.
Where do they come from?
The general consensus is that the original Roman numerals were influenced by the numerals of a neighbouring civilisation, the Etruscans, that inhabited modern day Tuscany. They used symbols which resembled their own alphabet, with some of them highlighted in the table on the right. It is thought they were adopted by the Romans around 500BC, who at this time were ruled by Etruscan kings, in an early form also highlighted in the table. They then morphed over time to become the symbols we know today. Where the original Etruscan numerals came from is unknown, although it has been suggested that they came from Attica in Greece, near Athens.
The way Roman numerals have been written over time has changed. The method of writing the number 4 as IV is a modern change, and in fact the majority of ancient and medieval sources we have found instead use the IIII notation. The same occurs with 9 and IX, with the first records of IX being used instead of VIIII not appearing until the 15th century. As well as that, often the numbers 13 and 16 were written with the smaller numerals in front, as IIIX and VIX respectively. This was done to preserve how the numbers were written in Latin, as ‘tertio decimo’ (three from ten) and ‘sexto decimo’ (six from ten) respectively.

Image credit: public domain via Ben Tocher.
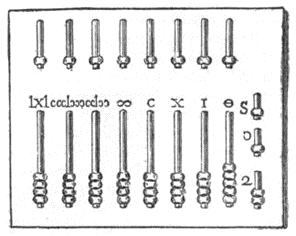
Image credit: Encyclopaedia Britannica, 9th ed., Vol. I, public domain via Wikimedia Commons.
How were they Used?
The Roman empire was one of the largest empires in world history, stretching from England to Egypt. To maintain such an extensive state, a mathematically literate population was needed to enforce taxes, conduct censuses, and organise military campaigns. Famously, Roman numerals are considered hard to conduct basic arithmetic with. In order to use them in calculations, the Romans used an abacus. The abacus works by having several lines of counters, each labelled with one of the base Roman numerals. The number of counters of each line denotes the number of that numeral required to write out the number. For example, the number 73 would contain one counter on the L line, two counters on the X line, and three counters on the I line. Some abacuses, such as in the example shown, will have two lines for each symbol, one representing a multiple of 5 of the symbols and one representing a multiple of 1 of the symbols. This was done to reduce the total number of counters needed. This device allowed engineers, accountants, and politicians to calculate using these symbols much more easily, as to add numbers you simply adjust the number of counters as you would with addition of Arabic numerals.
Cantor, Moritz, Vorlesungen über Geschichte der Mathematik (Leipzig, 1880), quoted in Cajori, Florian, A History of Mathematical Notations (Chicago, 1928)
Cappelli, Adriano, Lexicon Abbreviaturarum (Leipzig, 1901), quoted in Cajori, Florian, A History of Mathematical Notations (Chicago, 1928)
Chisholm, Hugh (ed.), Encyclopaedia Britannica Eleventh Edition (Cambridge, 1911)
Cuomo, Serafina, Ancient Mathematics (London, 2001)
Ruska, Julius, “Zur ältesten arabischen Algebra und Rechenkunst“, Sitzungsberichte d. Heidelberger Akademie der Wissensch (Philos.-histor. Klasse, 1917), quoted in Cajori, Florian, A History of Mathematical Notations (Chicago, 1928)
Tybjerg, Karin, ‘Technologies of Calculation, Part 3: Practical Mathematics’, in John Peter Oleson (ed.), The Oxford Handbook of Engineering and Technology in the Classical World (Oxford, 2008)
Schlimm, Dirk and Neth, Hansjörg, ‘Modelling Ancient and Modern Arithmetic Practices: Addition and Multiplication with Arabic and Roman Numerals’, in B. C. Love, K. McRae & V. M. Sloutsky (eds), Proceedings of the 30th Annual Conference of the Cognitive Science Society (July 2008), pp. 2097-2102
Author
Ben Tocher

