The Fibonacci Sequence
1,1,2,3,5,8,13,21 is a sequence you might recognise. Whether you learned about it in school, while reading the Da Vinci code, or in the TV series The Good Place; this very peculiar sequence has a hidden history. Where did it come from? Who discovered it? Why is it called the Fibonacci sequence? What is so special about it? Why does it repeatedly appear in popular culture?

Image credit: public domain via Wikimedia Commons.
Origins
Despite Leonardo Pisano, nicknamed ‘Fibonacci’, being the figure behind the name of the sequence, Fibonacci numbers can be traced back to approximately 450 BC in India. The earliest trace of the sequence is by poet and mathematician Acharya Pingala. Pingala is also credited with the first use of binary numbers, in his work Chandaḥśāstra, which is curiously the first known treatise of Sanskrit prosody, the study of poetic verses in Sanskrit. Relating back to the Fibonacci sequence, Pingala’s cryptic formula, named misau cha (“the two are mixed”) is its first appearance. When interpreted in context by scholars, Pingala’s formula related to the number of beats in poetic verses.
Other early appearances of the sequence are found in works by Bharata Muni, an ancient sage, in his study of Sanskrit performing arts (dating between 200BC and 200AD). However, perhaps the clearest expression of the sequence as we know it today is by Virahanka, an Indian prosodist (an expert in the elements of speech) and mathematician that lived around 700AD. Later, Acharya Hemachandra, a 12th century poet, mathematician and philosopher, also wrote about the sequence.
So, if the sequence was known for centuries before Pisano was even born, why was it named after him?
Leonardo Pisano, ‘Fibonacci’
Leonardo Pisano, commonly referred to as Fibonacci, was born circa 1170 in the city of Pisa, Italy. Growing up, he travelled around the Mediterranean frequently due to his father’s job directing a trading post in Algeria. During this time, he learnt various methods of arithmetic, including the Hindu-Arabic system.
Eventually, Pisano became a mathematician, and published his famous book called Liber Abaci, which showed practical uses of the Hindu-Arabic system. His book includes calculations of interest, converting weights and measures, amongst other practicalities of using the Hindu-Arabic system in contrast to Roman Numerals. Liber Abaci was well-received by other academics and had an important impact on mathematical thinking at the time. His mathematical advances also contributed to the exponential growth of accounting and banking in Europe. His work was so highly regarded by his community that the Republic of Pisa granted him a salary that recognised the services given to the city as an accounting advisor and teaching professional.

Image credit: Astriolok at English Wikipedia, Public domain, via Wikimedia Commons
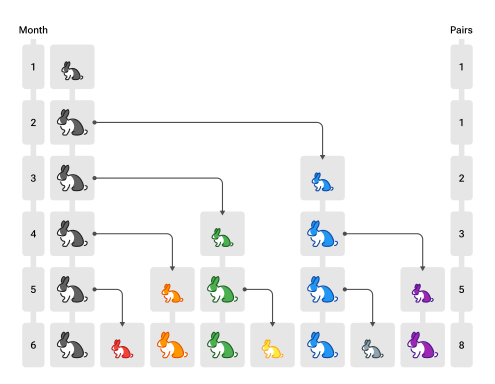
In his book Liber Abaci, Pisano proposed an exercise of rabbit population growth which led to the sequence being named after him. The exercise estimated the population growth of rabbits in a biologically impossible community after each month and again at the end of one year.
The exercise started with one pair of rabbits which mate during the first month, producing another rabbit at the end of the month, however there is still only one pair. At the end of the second month, the original pair produce another offspring, bringing the pair tally up to two. At the end of the third month, the original pair mate again, but so does the second pair, bringing the total pair tally to three. After the fourth month, the original pair mates again, but so does the second pair, and so there are now five pairs.
A pattern emerges, in which “at the end of the nth month, the number of pairs of rabbits is equal to the number of mature pairs (that is, the number of pairs in month n – 2) plus the number of pairs alive last month (month n – 1). The number in the nth month is the nth Fibonacci number”.
The Importance of the Sequence
Apart from its use in popular culture and media channels, the Fibonacci sequence holds special importance in other fields outside of mathematics and cinematography. This is mainly due its relation to the golden ratio: the number 1.618 033 988 749… . This specific ratio appears in many different natural settings, like shells, pineapples, animal flight patterns, rose petals, tree branches, etc. The ratio of two consecutive Fibonacci numbers increasingly tends towards the golden ratio. For example: 3/2 = 1.5, 5/3 = 1.67, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.615, etc. Other uses, however, also include technical analysis of financial data, which can be useful for traders to make and manage investments.
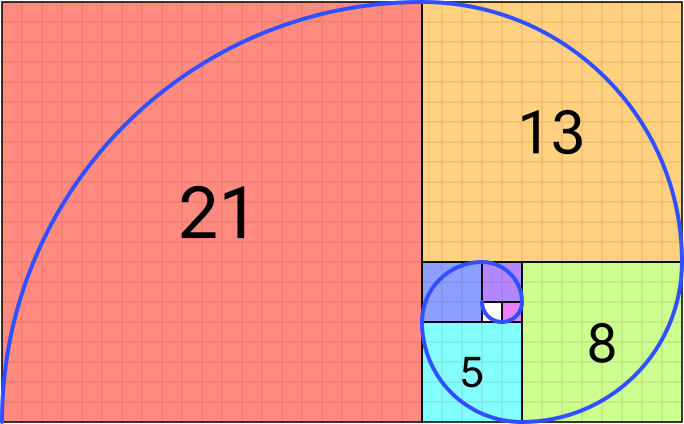
Image credit: Romain, CC BY-SA 4.0, via Wikimedia Commons

Image credit: Max Ronnersjö, CC BY-SA 3.0, via Wikimedia Commons
Australian Mathematical Sciences Institute. “History and Applications – Fibonacci Numbers.” History and applications – fibonacci numbers, 2000. https://amsi.org.au/ESA_Senior_Years/SeniorTopic1/1d/1d_4history_2.html#:~:text=1%2C%201%2C%202%2C%203,200%20BCE%20in%20Indian%20literature.
Goonatilake, Susantha. Toward a Global Science: Mining Civilizational Knowledge. Bloomington, IN: Indiana University Press, 1998.
Livio, Mario. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books, 2008.
O’Connor, J J, and E F Robertson. “Fibonacci – Biography.” Maths History (MacTutor), 1998. https://mathshistory.st-andrews.ac.uk/Biographies/Fibonacci/.
Sigler, Laurence Edward. Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation. New York: Springer, 2002.
Singh, Parmanand. “The so-called Fibonacci Numbers in Ancient and Medieval India.” Historia Mathematica 12, no. 3 (1985): 229–44. https://doi.org/10.1016/0315-0860(85)90021-7.
University of Utah Mathematics Department. “Liber Abacci.” Fibonacci’s Liber Abaci (book of calculation), 2005. https://www.math.utah.edu/~beebe/software/java/fibonacci/liber-abaci.html.
Wikipedia. “Fibonacci Number.” Wikipedia. Wikimedia Foundation, February 21, 2023. https://en.wikipedia.org/wiki/Fibonacci_number.
Author
Gustavo Velasco Melgar

