The Story of 𝜋 and Zu Chongzhi
Overview
The number 𝜋, one of the most well-known mathematical constants, is the ratio of a circle’s circumference to its diameter. It is an irrational number, meaning that it cannot be represented as a ratio of two integers, and it has infinitely many decimals. It is for this reason that the exact value of 𝜋 can never be calculated.
For over 4000 years, mathematicians all around the world have attempted to expand our understanding of 𝜋, sometimes by computing its value to a higher degree of accuracy. The renowned Chinese mathematician Zu Chongzhi was one of them. Around 480 AD, Zu Chongzhi calculated 𝜋 correct up to 7 decimal places (3.1415926 < 𝜋 < 3.1415927), setting up a world record that would remain unbeaten for over 900 years. Impressively, he used a highly advanced approach and underwent extremely complex calculations; interestingly, he was using merely a bunch of wooden sticks to perform his calculations.
Zu Chongzhi’s work on 𝜋
Apart from his approximation of 𝜋, Zu also introduced the Zu’s ratio (密率; milü): 𝜋 ≈ 355/113, which is the closest rational approximation to 𝜋 from all fractions with denominator less than 16600 (the next best rational approximation is 52163/16604 ≈ 3.1415923874). As pointed out by Japanese mathematician Yoshio Mikami, “milü could not be found in any Greek, Indian or Arabian manuscripts, not until 1585 Dutch mathematician Adriaan Anthonisz obtained this fraction; the Chinese possessed this most extraordinary fraction over a whole millennium earlier than Europe”.
So how did Zu derive his approximation of 𝜋 with such impressive accuracy? Zu adopted Liu Hui’s 𝜋 algorithm, which was invented by Chinese mathematician Liu Hui around 265 AD, to perform his calculations. A more detailed discussion of this algorithm and its similarity to Greek mathematician Archimedes’ 𝜋 algorithm can be found here. Zu ended up using a regular polygon with 24,576 (= 212 × 6) sides to approximate a circle and obtained his final result. According to the algorithm, this would require extremely lengthy calculations involving hundreds of square roots, all up to at least 9 decimal place accuracy. Remember, in Zu’s time there was no such thing as a handy calculator!
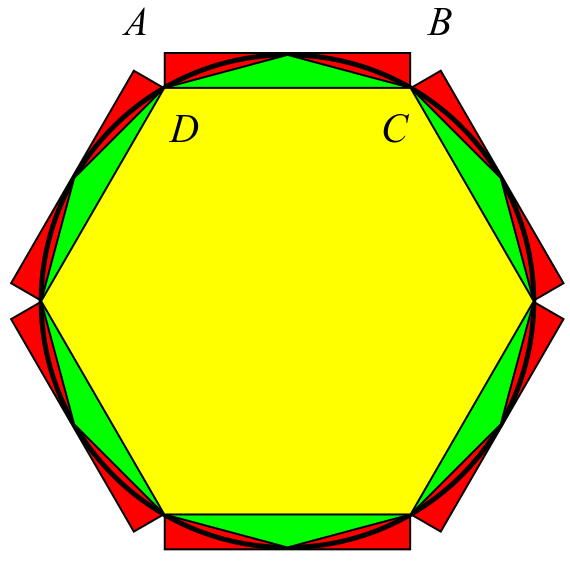
Image credit: Pbroks13, CC BY-SA 3.0 via Wikimedia Commons.
Tool for calculation in Zu’s time – Counting Rods
To perform his incredibly complex calculations, Zu recorded his intermediate steps by using only a pile of wooden sticks laid out in certain patterns. These sticks are called the counting rods (筹; chou), typically 3–14 cm (1″ to 6″) long. In fact, Chinese mathematicians started using them well over two thousand years ago.
Counting rods represent digits by the number and direction of the rods. To indicate the position of a digit, vertical and horizontal forms of rod numbers are used alternately: generally, vertical rods are used for the units, hundreds, ten-thousands, etc., whereas horizontal rods are used for the tens, thousands, hundred-thousands, etc.
Any rod perpendicular to the direction of the other rods represents 5. A blank space represents 0. And the colour plays a part here too, with red rods representing positive numbers and black rods representing negative numbers.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
Some examples:
| 238 | ||||
| 4096 | ||||
| -305 | ||||
| -6480 |
The written forms based on these are called the rod numerals, which are a true positional decimal numeral system, from the Warring States period of China (circa 475 BC) to the 16th century. Like the Roman numerals were used throughout the western world, the rod numerals were widely spread and adopted across ancient East Asia.
For further details on how to use the counting rods to represent numbers and perform calculations, a nice video can be found here.
Mikami, Yoshio, The Development of Mathematics in China and Japan (Leipzig, 1913).
O’Connor, John Joseph and Robertson, Edmund Frederick, ‘Zu Chongzhi’, MacTutor History of Mathematics Archive, Website, December 2003, <https://mathshistory.st-andrews.ac.uk/Biographies/Zu_Chongzhi/> [accessed 19 February 2023].
Shen, Kuo, Dream Pool Essays (1088).
Author
Yansong Li

